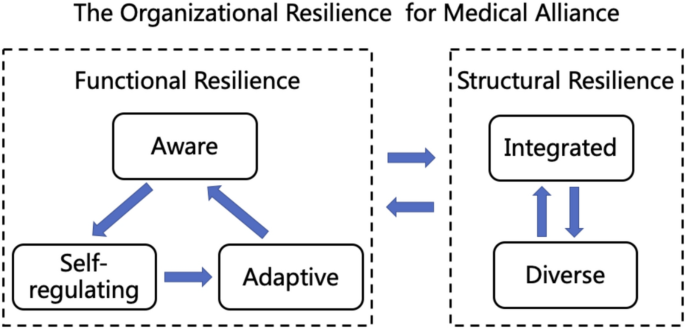
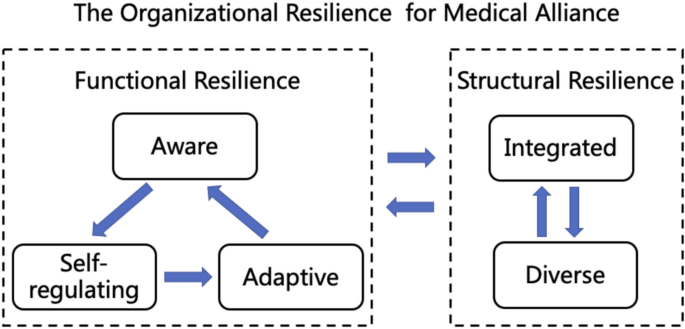
The model of organizational resilience factors for medical alliance
In this study, we construct the conceptual framework of health community organization resilience by referring to the 5 elements of health system resilience proposed by Professor Kruk. She indicated that the health system resilience should have the abilities of aware, diverse, self-regulating, integrated, and adaptive6. Huang and Wen believe that organizational resilience can be analyzed through a dual framework of structure and function15. Structural resilience refers to the ability of multiple agents within an organization to form a stable and enduring structure that performs specific functions. This involves two aspects: the diversity and integration of these multiple agents. Functional resilience, on the other hand, is the comprehensive capability of an organization to handle complex governance challenges. During the governance process, it manifests as a functional progression and a virtuous cycle through three stages: aware, self-regulating, and adaptive. Based on the above key articles, this study constructed a model of organizational resilience factors for medical alliances, and the 5 first-level sub-criteria are shown in Fig. 1.
The organizational resilience assessment framework for medical alliance.
Literature review and modeling process
A literature review was conducted using Web of Science, Science Direct, Google Scholar, PubMed, Wangfang, and CNKI. The retrieval period spanned from the inception of these databases to September 2023. We searched for literature using the following search terms: (resilience), (organizational resilience), (health system resilience), (medical group resilience), (hospital resilience), and (health care resilience). Inclusion criteria: (1) research topic focuses on the concept, connotation, and evaluation framework of organizational resilience within health systems or hospitals; (2) standardized and clear research methods and processes with reliable content; (3) research results include analysis and evaluation of resilience in health systems or hospital organizations. Exclusion criteria: (1) unclear definition of organizational resilience; (2) inadequate research methods relying on subjective judgment and unverifiable authenticity; (3) conference abstracts lacking full methodological disclosure.
Based on the selected literatures and group discussions, we constructed second-level and third-level sub-criteria for the organizational resilience of medical alliance (Table 1). Firstly, we identified and marked keywords related to organizational resilience, analyzed their frequency and occurrence rate, and selected important keyword with a frequency > 5% and an occurrence rate > 15%. “Frequency” indicates the number of times a keyword appears, while “occurrence rate” is the proportion of a keyword’s appearances relative to all keywords, calculated as occurrence rate = frequency/total number of keywords16. These were classified into five first-level sub-criteria frameworks, resulting in 15 second-level sub-criteria through group discussions. Secondly, we formed an initial pool of sub-criteria was formed by collecting and summarizing relevant evaluation indicators of organizational resilience from the selected literatures. Our research group screened these sub-criteria, sorted and organized them based on first-level and second-level sub-criteria frameworks. Then five experts (two university professors, two hospital directors and one director of health administration department) and our research group conducted two rounds of discussions to finalize the 43 three-level sub-criteria (Table 1, Fig. 2). Finally, we obtained the weights and rankings of the first-, second-, and third-level sub-criteria through a survey of 19 experts from universities, health commissions, centers for disease control and preventions (CDC), and hospitals using the AHP method, thereby identifying the critical factors.
The hierarchical structure of AHP for organizational resilience assessment. *Indicates subjective items; the rest are objective items.
The analytic hierarchy process method
AHP is a sophisticated method for subjective decision-making, pioneered by Saaty in the early 1970s31. The AHP method is valuable for its ability to structure complex decisions, involve multiple perspectives, and provide a quantitative framework for evaluating qualitative criteria, leading to more informed and objective decision-making processes. The AHP involves several steps: First, structure the decision problem into a hierarchy with a clear goal, criteria, and alternatives. Next, conduct pairwise comparisons of the criteria to assess their relative importance using a nine-point scale. Then, calculate the weights for each criterion to represent their significance in relation to the others. After that, synthesize the priorities to determine an overall score for each alternative by combining the criteria weights with the alternatives’ scores. It’s crucial to perform a consistency check using the consistency ratio to ensure the judgments made in the pairwise comparisons are consistent; if the ratio exceeds a certain threshold, the comparisons may need revision. Finally, based on the calculated scores and rankings, the alternative with the highest score is selected as the best option31,32.
The steps of the AHP in this study are as follows:
Step 1 Define and state the organizational resilience for medical alliance clearly. The hierarchal structure of organizational resilience is divided into three levels, including 5 first-level sub-criteria, 15 second-level sub-criteria, and 43 third-level sub-criteria.
Step 2 Obtain the paired comparison matrix from each expert. According to the consistent matrix method proposed by Saaty et al., a judgment matrix A for pairwise comparison is constructed using the relative importance scores of pairwise indicators at the same level, as provided by expert consultation, as shown in Eq. (1). The element α of the paired comparison matrix is determined by Saaty’s 9-point Likert scale (from “equally important” to “absolutely important”).
$$A = \left( {a_{ij} } \right) = \left[ {\begin{array}{*{20}c} {a_{11} } & \cdots & {a_{1j} } \\ \vdots & \ddots & \vdots \\ {a_{i1} } & \cdots & {a_{ij} } \\ \end{array} } \right],$$
(1)
Step 3 Calculate the relative weights between criteria. Formula (2) is used to calculate the product \({M}_{i}\) of each row element in the paired comparison matrix. Formula (3) is used to calculate the n-th root of \({M}_{i}\), where n is the order of the matrix. Formula (4) is used to obtain the eigenvector \({W}_{i}\) of each matrix, and further determine the influence degree of each index on the resilience of the organization.
$$M_{i} = {\Pi }a_{ij} ,\; ij = 1, 2 , \ldots , n$$
(2)
$$Y_{i} = \left( {M_{i} } \right)^{\frac{1}{n}} ,$$
(3)
$$W_{i} = \frac{{Y_{i} }}{{\sum Y_{i} }}$$
(4)
Step 4 Check the consistency of the paired comparison matrix provided by each individual expert. The random consistency ratio (CR) for each expert’s judgment matrix is used to test the consistency of that expert’s scores. When CR < 0.1, it indicates that the expert’s constructed judgment matrix has satisfactory consistency. When CR ≥ 0.1, the minimum forward method and the maximum change method are used to make corrections. For each expert’s matrix, the general consistency index (CI) is calculated by formula (5), where \({\uplambda }_{max}\) is the largest eigenvalue of the paired comparison matrix. Formula (6) is used to calculate the random CR. For different matrix sizes, the respective values of the random consistency (RI) index are shown in Supplementary Table S1. Only judgement matrices from experts achieving CR < 0.1 were included in the subsequent aggregation process.
$$CI = \frac{{\lambda_{max} – n}}{n – 1},$$
(5)
$$CR = \frac{CI}{{RI}}$$
(6)
Sensitivity analysis
To evaluate the robustness of the AHP weights derived from the expert data, a sensitivity analysis was conducted using a Monte Carlo simulation approach to perturb the expert authority levels. First, the AHP weights were structured for computational processing, with baseline authority values assigned to each expert. Second, a Monte Carlo simulation with 10,000 iterations was executed. In each iteration, the expert authority levels were randomly adjusted by ± 10% of their base values. Third, in each iteration, the AHP weights were recalculated using the adjusted expert authority levels. Fourth, the stability of the weights was assessed by measuring the fluctuation of each weight across all iterations. The 95%CI for each weight were recorded, and the percentage change relative to the original weight was calculated.
Data collection
This study was carried out from August to September 2023, the expert questionnaire was sent by email for two rounds, and respondents were asked to complete the survey within 10 days for each round. Based on the outcomes of the first round of expert consultation and the feedback provided by the experts, the indicator system for organizational resilience of medical alliance was revised, and the foundation for the second round of expert consultation was established. In the second round, the experts’ relative importance scores for the pairwise comparisons between indicators at the same level were aggregated to determine the final weight coefficients for the indicators at each level.
The selection of the 19 experts in the study considered factors such as geographical location, occupation type, and age distribution to ensure the representativeness of their views. Geographically, the experts were drawn from northern provinces (n = 6), southeastern provinces (n = 8), and southwestern provinces (n = 5) of China, representing first-tier cities, coastal areas, and western mountainous districts, respectively. This distribution reflects China’s socioeconomic gradient. In terms of occupation type, the experts included individuals from scientific research institutions (n = 6), health administration departments (n = 6), and hospitals (n = 7), covering both management and technical roles. Regarding age distribution, the experts ranged in age from 37 to 63 years old. The selection criteria for the participants were as follows: (1) more than 5 years of working experience in the field of medical alliance; (2) management and technical experts on the organizational resilience; (3) can actively and voluntarily participated in this consultation. This study met the requirements of the AHP analysis method.
Ethical issues
This study was conducted in accordance with the 1964 Declaration of Helsinki and received the approval of the Ethics Committee of Hangzhou Normal University Ethics Board (No.2019065). Informed consent was obtained from all individual participants included in the study.
link