Validation of an interactive process mining methodology for clinical epidemiology through a cohort study on chronic kidney disease progression

We proposed a framework for applying process mining discovery in observational longitudinal epidemiology studies involving eight steps, as shown in Fig. 1. The workflow consists of two main parts: the traditional epidemiological study process is shown in grey, and the blue section signifies data-driven process mining. All the steps are described specifically in Sect. 2.1 to 2.8.

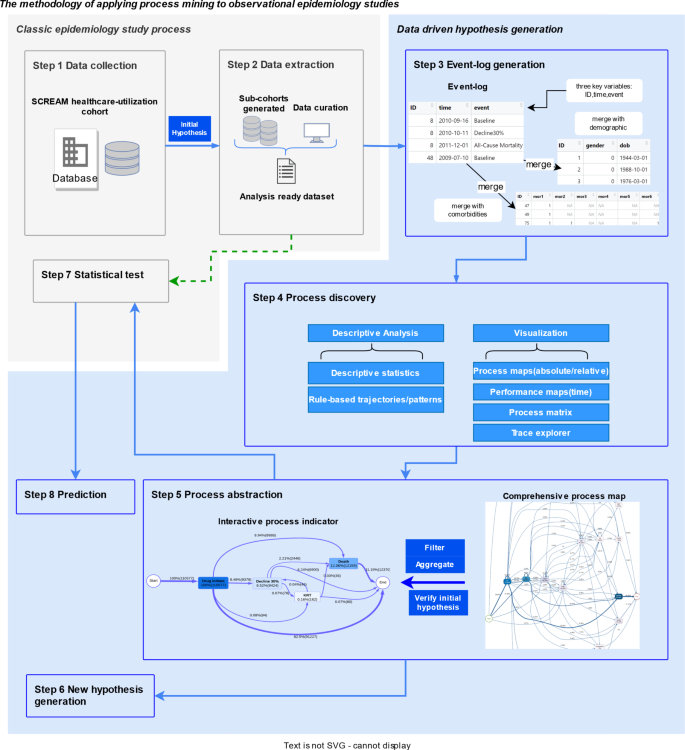
Proposed methodology workflow of process mining applied to observational epidemiology studies: The solid arrow illustrates the case study explored in this paper. The green dotted arrow represents the classic epidemiological study process, which is not performed in the current study.

Real-world database and setting

The first step in this methodology is to have a relevant real-world database that contains information about the event of interest, including timestamps for each event occurrence.

In this study, we used data from the Stockholm CREAtinine Measurements (SCREAM) database¹² includes comprehensive laboratory and healthcare data from over 1.1 million adult residents in Stockholm, collected from 2006 to 2011, focusing on chronic kidney disease and associated healthcare outcomes. Medications are identified by recorded pharmacy dispensations through the Anatomical Therapeutic Classification (ATC) codes from linkage with the Swedish Prescribed Drug Registry. This study was conducted in accordance with the Declaration of Helsinki. Approval for the study was obtained from the Swedish National Board of Welfare and the Stockholm Regional Ethics Review Board, who deemed that informed consent was not required and provided de-identified data.

Data extraction and curation

Data preprocessing, including cleaning and transformation, is a critical initial step to render the dataset compatible with process mining techniques. After preprocessing, the “analysis-ready dataset” necessitates including at least three key variables: patient ID, event or state, and the corresponding event occurrence time.

In this study, we built a retrospective cohort of new users of PPI and H2 blockers (H2B) from SCREAM. The index date was defined as the first dispensation date of PPI or H2B between 2007 and 2010. We included individuals who had newly initiated PPI or H2B and had at least a recorded serum/plasma creatinine test in connection with an outpatient consultation no more than one year before the index date. The definitions follow the same approach as previously published from the same data source¹¹, which uses traditional statistical methods to compare the reproducibility of findings with the proposed process mining approach. New users were thus defined as the first-time PPI or H2B dispensed between January 1, 2007 (records in 2006 were used to ensure at least 12 months with no recorded use of these medications) and December 31, 2010 (records in 2011 were used to ensure at least one year follow up time to detect the effect); Individuals were excluded if (a) estimated glomerular filtration rate (eGFR) < 15 mL/min/1.73 m² (The calculation of eGFR used the Chronic Kidney Disease Epidemiology Collaboration (CKD-EPI) 2009 creatinine Eq.(¹³); and (b) age < 18 years old.

The transition states were defined as (1) Drug (PPI/H2B) initiation; (2) an eGFR decline > = 30% relative to baseline eGFR, which defines a clinically meaningful drop in eGFR that has been accepted as a surrogate endpoint of CKD progression by regulatory agencies of drug approvals¹⁴; (3) Kidney replacement therapy (KRT), which is ascertained by linkage with the Swedish Renal Registry and includes both the date of kidney transplant and the date of start of maintenance dialysis; (4) All-cause mortality. If no events were observed by the end of the study (2011-12-31) or the participant emigrated from the Stockholm region, they were labelled as censored.

Independent covariates were ascertained on the index date, including age, gender and baseline eGFR. Baseline eGFR was defined as the most recent measurement before or on the PPI/H2B dispensation date. Time-dependent covariates included comorbidities and concomitant medications. Time-dependent comorbidities were identified based on diagnostic records available up to and including the event date. This study considered the following comorbidities as potential indications for acid-suppressive therapy: gastroesophageal reflux disease, Barrett’s esophagus, ulcer disease, helicobacter pylori infection, and upper gastrointestinal bleeding. Additionally, we investigated the following comorbidities to assess their influence: hypertension, diabetes mellitus, myocardial infarction, congestive heart failure, peripheral vascular disease, cerebrovascular disease, and COPD. Time-dependent concomitant medications were extracted based on dispensation records from the six months preceding each event. These medications included nonsteroidal anti-inflammatory drugs (NSAIDs)/aspirin, statins, and antithrombotics. The ICD-10 codes of included comorbidities and the ATC codes of PPI/H2B were summarised in Supplementary Table 1. Data management was conducted using R x64 4.1.2.

Event-log generation

Process mining event log was generated based on the analysis-ready dataset, in which each row represents a single event and a single timestamp.

In our case study, we uploaded the analysis-ready dataset to R and employed the event-log generation function provided by an R package bupaR¹⁵ to produce the event-log necessary for subsequent process model development. For further analysis, we can merge the demographic or comorbidities dataset to the event-log when necessary. Other packages or applications, such as PmineR¹⁶, PMApp¹⁷, and ProM¹⁸, could also be employed for this purpose.

Process discovery

Process discovery⁵ is the critical technique used to depict the process from the data into graphical workflows. A process discovery algorithm or miner serves to derive the process model. In the healthcare domain, prevalent process discovery algorithms/miners encompass “PALIA”, “Inductive Miner”, and “Care Flow Miner”⁵. Utilising the process model, we can conduct descriptive analyses, such as descriptive statistics and rule-based patterns, and visualise the process maps, process matrix, and trace explorer.

In the current case study, the process discovery algorithm/miner employed was the Directly-Follows Graph (DFG), which is a key component of the bupaR package¹⁵. This algorithm/miner facilitates the extraction of process models based on the time-sequential relationships between activities within an event log.

Process abstraction

The complexity of disease event logs often results in initial process models exhibiting complicated relationships between events and traces, occasionally resembling a process map of high complexity commonly known as a ‘spaghetti’ pattern¹⁹. Such complexity presents significant challenges for researchers attempting to understand the process and derive meaningful insights from its elaborate configuration. The process abstraction aims to turn the process map mined in the process discovery process into a simpler, understandable and focused process model that can be used to study the process under analysis.

Consequently, using interactive process indicators (IPIs)²⁰ for abstracting the process can provide a clear, human-understandable view by focusing on the essential parts of the process. A process indicator (PI) is defined as a visual representation of a process, i.e., a process map, functioning as an indicator to measure and comprehend that process²⁰. IPIs emerge from applying the interactive paradigm in collaboration with domain experts to generate process indicators²⁰. Some strategies, such as sampling²¹, clustering²², and a deep learning-based method²³, can be used to abstract simpler process models from complex event data with acceptable precision. One of the most commonly used techniques for abstraction is filtering²⁴, which allows the selection of relevant events and pathways, thereby focusing on the key aspects of the process. Filtering can also be employed to stratify PIs for different patient subgroups based on their characteristics, enabling comparative analysis. Moreover, filtering helps reduce noise by eliminating irrelevant data. Another strategy is aggregation, where multiple distinct events are combined into a higher-level event, simplifying the process model without sacrificing critical information.

In the context of our case study, we applied filtering to the primary process model to stratify PIs for patients based on their use of PPI or H2B. The specific events representing key stages of disease progression were confirmed by an expert in clinical kidney disease epidemiology. We further aggregated two events (CKD Decline by 30%, KRT) into a single event (Decline 30% or KRT) for statistical modelling due to the limited number of KRT events. The choice of abstracting IPIs through filtering and aggregation was guided by the research question and clinical relevance. This approach ensured that no data were wasted while maintaining an accurate reflection of the real-world disease progression pathways. Additionally, filters were applied to stratify IPIs based on comorbidities, allowing us to further evaluate the association between comorbid conditions and kidney function progression trajectories.

New hypothesis generation

Beyond the initial hypotheses, the process model analysis derived from the previous step 2.5, may provide new insights from the data.

Test the hypothesis with the statistical method

The process model offers valuable visualisations and parameters to primarily verify the initial hypotheses. Statistical tests or models based on the data characteristics were conducted to ensure a better understanding and meaningful interpretation of the results.

In this case study, baseline characteristics were presented as mean and standard deviations for continuous variables or median and interquartile range (IQR) for continuous variables but with skewed data.

A multistate model was constructed based on the process model obtained in 2.4 to quantify and interpret the observed transitions comprehensively. This model was formulated as a continuous-time Markov process for modelling CKD progression, under the Markov assumption that future transitions depend only on the current state. The Markov assumption is considered suitable for modelling CKD progression because, in clinical practice²⁵, nephrologists and clinical guidelines emphasise the current eGFR stage when determining treatment strategies. Additionally, previous studies^26,27 on CKD progression have used multistate Markov models to estimate progression rates and identify risk factors, providing support for the appropriateness of this assumption in the current context. We later incorporated time-dependent covariables to relax the assumption of time-homogeneous, allowing for transition rates that may vary over time, better capturing the complexity of CKD progression. The multistate model developed in this study incorporated covariates, as outlined in Sect. 2.2, to account for their potential influence on disease progression transitions. Adjusted hazard ratios, along with corresponding 95% confidence intervals (CIs), were used to estimate the effects of these covariates on the transition probabilities between disease states. The multistate model in this study is constructed as follows:

The msm²⁸ package for multistate modelling in R was used. Data analysis was conducted using R x64 4.1.2.

Prediction

The transition intensity of the process model was quantified using a multistate model in step 2.7. After deriving this multistate model, we were able to predict a specific event/state at a future time or a given individual²⁸.

In our case study, we developed a “Risk prediction” tool ( based on the process model and multistate model using R shiny 1.7.5.